მეოთხე ეპიზოდის გარჩევები pdf ფორმატში. ეს კი upsolving-ის ბმული :)
| # | ამოცანა | ავტორი |
| A | discount | ელდარ ბოგდანოვი |
| B | chocolate | ანდრეი ლუცენკო |
| C | friends | დავით რაჭველიშვილი |
| D | rect | ელდარ ბოგდანოვი |
| E | polyline | ელდარ ბოგდანოვი |
ამოცანა A. "ფასდაკლება"
ამოხსნის ძირითადი ნაწილია მოცემულ სიტყვაში განსხვავებული ასოების რაოდენობის დათვლა. მოცემული შეზღუდვების (სტრიქონის სიგრძე არ აღემატება 15-ს) პირობებში, ამის გაკეთება მრავალი გზით შეიძლება. მე მოვყვები ისეთს, რომელიც ძალიან გრძელი სტრიქონებისთვისაც სწრაფად მუშაობს. ერთადერთი შეზღუდვა ამ მიდგომაზე არის ანბანის (ანუ სხვადასხვა სიმბოლოთა რაოდენობის, რომლისგანაც შეიძლება სტრქონი შედგებოდეს) შედარებით მცირე ზომა.შევქმნათ bool მასივი იმდენი ელემენტით, რამდენიცაა ანბანის ზომა. ამ მასივში ჩვენ აღვნიშნავთ, ანბანის i-ური სიმბოლო შეგვხვდა თუ არა სტრიქონში. შემდეგ გავუაროთ მთელ სტრიქონს და თითოეული სიმბოლოსთვის ჩვენი მასივის შესაბამის ელემენტში ჩავწეროთ მნიშვნელობა true. ცხადია, ბოლოს ამ მასივში რამდენი true-ც გვექნება, ისაა განსხვავებული ასოების რაოდენობა. ეს მიდგომა შეგვიძლია განვაზოგადოთ სტრიქონში ყოველი სიმბოლოს სიხშირის დასათვლელად და მთელ რიგ მსგავს ამოცანების ამოსახსნელად.
გარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.
ამოცანა B. "შოკოლადი"
ეს ამოცანა არ მოითხოვს რამე განსაკუთრებულ ალგორითმს, პირდაპირი სიმულაცია მოგვცემს შედეგს და უპრობლემოდ ჩაეტევა დროში. შემოვიღოთ ორი მთელი ტიპის ცვლადი n, m, რომლებშიც შევინახავთ შოკოლადის ფილის მიმდინარე სიგანეს და სიმაღლეს. ყოველ შემოსულ C i ბრძანებაზე ვარკვევთ C-ს მიხედვით სიგანეს უნდა დავაკლოთ თუ სიმაღლეს. ვთქვათ სიგანეს, მაშინ n-ს უნდა დავაკლოთ min(i,n-i), თუ სიმაღლეს, მაშინ m-ს უნდა დავაკლოთ min(i,m-i).
ყველა ოპერაციის შესრულების შემდეგ n და m ცვლადებში პირდაპირ გვექნება ამოცანის პასუხი და გამოვიტანთ მას.
გარჩევა მომზადებულია ანდრეი ლუცენკოს მიერ.
ამოცანა C. "მეგობრები"
ამოცანაში მოცემული შეზღუდვები გვაძლევს საშუალებას, რომ მარტივი მოდელირებით ამოვხსნათ იგი და არ ვიფიქროთ ოპტიმიზაციებზე. შემოვიღოთ ორგანზომილებიანი მასივი, რომელშიც (i,j) პოზიციაზე შევინახავთ სტატუსს ამ ნომრების მქონე სისტემის მომხმარებლების მეგობრობაზე. ასევე საჭირო იქნება კონკრეტული სახელის მქონე ადამიანის ნომრის დადგენა, რისთვისაც გამოვიყენებთ Map
ჩვენს მიერ შედგენილი მოდელში მეგობრებში დამატებისა და წაშლის იმპლემენტაცია მოხდება O(1) დროში, შესაბამისი მატრიცის ელემენტში 1ის ან 0ის მინიჭებით. ხოლო SUGGEST name ოპერაციისათვის საჭიროა გადავარჩიოთ ყველა შესაძლო მომხმარებელი რომელიც არ არის name-ის მეგობარი და მასთან ყველაზე მეტი საერთო მეგობარი ყავს და თუ ესეთი რამოდენიმეა მაშინ ლექსიკოგრაფიულად მინიმალურს ამოვარჩევთ.
გარჩევა მომზადებულია დავით რაჭველიშვილის მიერ.
ამოცანა D. "მართკუთხედები"
პირველ რიგში შევნიშნოთ, რომ იმ კვადრატის გვერდი, რომელსაც K დაყოფის შემდეგ ვღებულობთ, ზუსტად N=2^K ცალ ერთეულოვან კვადრატს შეიცავს.
მართკუთხედების საერთო რაოდენობის ფორმულა შეიძლება რამდენიმენაირად გამოვიყვანოთ:
1) ყოველი ერთეულოვანი კვადრატისთვის დავაკვირდეთ, ისეთი რამდენი მართკუთხედი აიგება, რომ ზედა მარცხენა კუთხე მოცემულ კვადრატში ჰქონდეს. ფაქტიურად ეს რაოდენობა მოცემული კვადრატისგან არამარცხნივ და არაზემოთ მოთავსებული კვადრატების რაოდენობის ტოლია. გადავნომროთ კვადრატები 1-დან N-ის ჩათვლით ზემოდან ქვემოთ და მარცხნიდან მარჯვნივ და დავარქვათ i-ური რიგის j-ურ კვადრატს (i,j). (1,1)-ისთვის გვაქვს N^2 ცალი მართკუთხედი, (1,2)-სთვის - N*(N-1), (1,3)-ისთვის N*(N-2) და ასე შემდეგ. (2,1)-ისთვის გვაქვს ისევ N*(N-1), (2,2)-ისთვის (N-1)^2, (2,3)-ისთვის (N-1)*(N-2) ცალი. საზოგადოდ, (i,j)-სთვის გვაქვს (N-i)*(N-j) ცალი მართკუთხედი, რომელსაც (i,j)-ში აქვს ზედა მარცხენა კუთხე. რომ ავჯამოთ ყოველი კვადრატისთვის მიღებული რაოდენობა, მივიღებთ ჯამს N^2+2*N*(N-1)+2*N*(N-2)+...+(N-1)^2+2*(N-1)*(N-2)+... . ადვილი დასანახია, რომ ეს 1-დან N-მდე რიცხვების ჯამის კვადრატია. თვითონ 1-დან N-მდე რიცხვების ჯამი კი არითმეტიკული პროგრესიის ფორმულით (1+N)*N/2-ის ტოლია. შედეგად, ამოცანის პასუხი (N*(N+1)/2)^2 არის.
2) შეგვიძლია ეს ფორმულა სხვანაირადაც მივიღოთ. დავყოთ მართკუთხედები ოთხ კატეგორიად: ერთეულოვანი კვადრატები, 1xM სახოს ზოლები, Mx1 სახის ზოლები და ყველა დანარჩენი. პირველი კატეგორიის მართკუთხედი სულ N^2 ცალია - სულ ამდენი ერთეულოვანი კვადრატი გვაქვს დაფაზე პროცესის ბოლოს. მეორე კატეგორია ჰორიზონტალური ზოლებია 1-ზე მეტი სიგრძის. ფიქსირებულ ჰორიზონტალში რომ ავიღოთ განსხვავებულ კვადრატთა წყვილი, ის ერთ ზოლს განსაზღვრავს. სულ წყვილების რაოდენობაა N*(N-1)/2, ხოლო ჰორიზონტალები ჯამში N ცალი გვაქვს. აქედან ასეთი ზოლების რაოდენობა N*N*(N-1)/2 გამოდის. ანალოგიური მსჯელობით, ვერტიკალური ზოლების რაოდენობასაც ამდენს მივიღებთ. დაგვრჩა მეოთხე კატეგორია. მასში შედიან ისეთი მართკუთხედები, რომლებიც ორივე განზომილებაში 2 მაინც კვადრატს შეიცავენ - ანუ მარცხენა და მარჯვენა გვერდიც განსხვავებულ სვეტშია და ქვედა და ზედაც განსხვავებულ სტრიქონშია. ყოველი კვადრატისთვის, გვაქვს (N-1)^2 კვადრატი, რომელიც მისგან განსხვავებულ სტრიქონსა და სვეტშია. სულ N^2*(N-1)^2 ცალი მართკუთხედი გამოდის. თუმცა ამ დათვლაში ყოველი მართკუთხედი 4ჯერაა ჩათვლილი: მათ 4 კუთხური კვადრატი აქვთ და ეს ოთხივე კვადრატი თავისთან მიითვლის. ანუ ჯამში N^2*(N-1)^2/4 ცალი მეოთხე კატეგორიის მართკუთხედია. ავჯამოთ 4ივე კატეგორიის მართკუთხედების რაოდენობა და მივიღებთ ისევ (N*(N+1)/2)^2-ს.
3) მართკუთხედის ჩარჩო წარმოადგენს ორი (არა აუცილებლად განსხვავებული) ჰორიზონტალის და ორი (კვლავ შეიძლება ტოლი) ვერტიკალის თანაკვეთას. სულ გვაქვს N*(N+1)/2 წყვილი ჰორიზონტალი და ამდენივე ვერტიკალი. შესაბამისად, პასუხი (N*(N+1))-ია.
გარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.
ამოცანა E. "ტეხილი"
უპირველესყოვლისა შევნიშნოთ, რომ ტეხილში მონაკვეთების მიმდევრობას მნიშვნელობა არა აქვს. პასუხს ცვლის მარტო ის, მონაკვეთს ტეხილს ერთი ბოლოთი მივუერთებთ თუ მეორეთი. კერძოდ, თუ გვაქვს ტეხილის რაღაც ფრაგმენტი, რომლის ერთი ბოლო არის (X,Y) წერტილში და მაგ წერტილში (a,b)-თი განსაზღვრულ მონაკვეთს ვუმატებთ, მისი ერთი ბოლოთი მიერთებისას ტეხილის ბოლო გადავა წერტილ (X+a, Y+b)-ში, ხოლო მეორე ბოლოთი მიერთებისას - (X-a, Y-b)-ში. უკვე ამ დაკვირვების საფუძველზე ჩვენ შეგვიძლია O(2^N) სირთულის ალგორითმი შევქმნათ, რომელიც ყოველი მონაკვეთის ან ერთი, ან მეორე ბოლოთი მიერთებას შეეცდება და საუკეთესო პასუხს იპოვის. თუმცა N=100-ისთვის ეს მიდგომა არარეალურია.
ეს ამოცანა, უფრო ზოგადად დასმულიც კი (როდესაც კოორდინატები არამთელ შემოუსაზღვრელ რიცხვებში შეიძლება იყოს), შეიძლება ამოიხსნას წმინდა გეომეტრიულად. ჩვენი მონაკვეთები რეალურად ვექტორებს წარმოადგენენ და მათი ტეხილზე ერთი ან მეორე ბოლოთი მიერთება ტოლფასია მათი ნიშნის ცვლილების. დავარქვათ ჩვენს ვექტორებს v1, v2, ..., vN. მათ მიერ შედგენილი ტეხილის ერთი ბოლოდან მეორეში გაჭიმული ვექტორი V იქნება ტოლი:
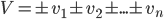
ოპტიმალურ ამოხსნაში, არც ერთი ვექტორისთვის ნიშნის შეცვლამ უკეთესი პასუხი არ უნდა მოგვცეს, ანუ ყოველი დადებითი ნიშნით აღებული ვექტორისთვის სრულდება:
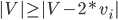 , სადაც |X| X ვექტორის სიგრძეს აღნიშნავს.
, სადაც |X| X ვექტორის სიგრძეს აღნიშნავს.
ავიყვანოთ ეს უტოლობა კვადრატში და მივიღებთ:
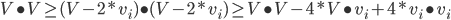
აქედან 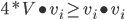 და ვინაიდან
და ვინაიდან 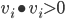 ნებისმიერი არანულოვანი ვექტორისთვის, დადებითნიშნიანი ვექტორებისთვის გამოგვდის
ნებისმიერი არანულოვანი ვექტორისთვის, დადებითნიშნიანი ვექტორებისთვის გამოგვდის 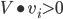 .
.
ანალოგიური მსჯელობით უარყოფითნიშნიანი ვექტორებისთვის, მივიღებთ 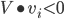 .
.
ანუ დავადგინეთ, რომ ოპტიმალური ტეხილისთვის არსებობს V=0 პირობით განსაზღვრული წრფე, რომლის ერთ მხარეს მოთავსებული ვექტორები დადებითი ნიშნით უნდა ავიღოთ, ხოლო მეორე მხარეს მოთავსებულები უარყოფითით. შედეგად, რომ განვიხილოთ ყველა შესაძლო წრფე და დავითვალოთ პასუხი ვექტორების შესაბამისი განლაგებისთვის, მათ შორის მაქსიმალური იქნება ამოცანის პასუხიც. რეალურად წრფეების რაოდენობა უსასრულოა, მაგრამ ჩვენ გვაინტერესებს მხოლოდ ისეთი წრფეები, რომლებიც ვექტორების განსხვავებულ სიმრავლეებს ტოვებენ სხვადასხვა მხარეს - ასეთი კი სულ N ცალია. ასე რომ ამოცანა შეიძლება O(N^2) სირთულის ალგორითმით ამოიხსნას.
ამ კონკრეტულ ამოცანაში ჩვენი მონაკვეთის ბოლოები მთელკოორდინატებიან რიცხვებს წარმოადგენენ, რომლებიც მოდულით არ აღემატებიან 1000-ს. ეს საშუალებას გვაძლევს, დინამიურ პროგრამირებას მივმართოთ. შევეცადოთ, "ავაშენოთ" ტეხილი მონაკვეთების თანდათან დამატებით. ჩავთვალოთ, რომ ტეხილის ერთი ბოლო (0,0) წერტილში არის. მონაკვეთების დამატებამდე, ტეხილის მეორე ბოლოც მხოლოდ (0,0)-ში შეიძლება იყოს მოთავსებული. ვთქვათ, პირველი მონაკვეთია (X,Y). იგი შეიძლება ან ერთი ბოლოთი მივუერთოთ ტეხილს, ან მეორით, შედეგად ტეხილის მეორე ბოლო იქნება ან წერტილში (X,Y), ან წერტილში (-X,-Y). მეორე მონაკვეთისთვის მიერთების კანდიდატებად უკვე ამ ორ წერტილს განვიხილავთ, და ასე შემდეგ. ანუ, ყოველი მონაკვეთის დამატების წინ უნდა გვქონდეს შენახული ყველა განსხვავებული წერტილი, სადაც შეიძლება იყოს ტეხილის მეორე ბოლო და ამ ყოველი ასეთი წერტილისთვის უნდა ვცადოთ მიმდინარე მონაკვეთის ერთი ან მეორე ბოლოთი მიერთება ამ წერტილზე. ამოცანის პასუხის მისაღებად ბოლო მონაკვეთისთვის მიღებული შესაძლო ბოლოების სიმრავლიდან უნდა ამოვირჩიოთ ისეთი (X,Y) წერტილი, რომლისთვისაც X^2+Y^2 მაქსიმალურია.
ვინაიდან სულ გვაქვს 100-მდე მონაკვეთი კოორდინატებით -1000-იდან 1000-მდე, ბოლო მონაკვეთებისთვის ტეხილის მეორე ბოლოს კოორდინატები შეიძლება -100000-დან 100000-მდე იყონ და ჯამში 200001^2 სხვადასხვა კანდიდატი გვექნება. რა თქმა უნდა, ესეც ძალიან დიდი რიცხვია. მაგრამ რეალურად ჩვენ არ გვჭირდება ყველა ამ წერტილის დამახსოვრება. ჩვენ X^2+Y^2-ის მაქსიმიზაციას ვახდენთ, ამიტომ ყოველი კონკრეტული X-სთვის საკმარისია შევინახოთ მხოლოდ უდიდესი და უმცირესი Y (უმცირესი იმიტომ, რომ უარყოფითი Y-ებისთვის Y^2 შეიძლება საუკეთესო დადებითისას აღემატებოდეს). ამრიგად, მაქსიმუმ 200001*2 წერტილი უნდა დავიმახსოვროთ, ხოლო ალგორითმის სირთულე O(N^2 * XMAX) არის, სადაც XMAX მონაკვეთების ბოლოების დიაპაზონის ზომაა.
შეგვიძლია ამ ანალიზში კიდევ უფრო შორს წავიდეთ და შევნიშნოთ, რომ კონკრეტული X-ისთვის მხოლოდ უდიდესი Y-ის დამახსოვრებაც კმარა. მკითხველს ვთავაზობ, დამოუკიდებლად დაადგინოს, თუ რატომ არის ასე.
გარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.





გვერდის პარალელური." ეს მონაკვეთი დასაზუსტებელია, ამ მოცემულობისთვის ერთხელ შეიძლება ერთი მხრიდან მოატეხოს ლილუმ ფილას, მეორედ - მეორე მხრიდან, ცხადია რომ გადატეხვის ზოლიდან დაშორება გვერდებისადმი იქნება სხვადასხვა, უნდა იყოს მითითებული რომელი მხრიდან ტყდება შოკოლადს ფილა. ესაა ჩემი აზრით ამოცანის პირობაში უზუსტობა, და თუ შეიძლება რომ გამოეხმაუროთ ჩემს კომენტარს და დამეხმაროთ ამოცანის პირობის გარკვევაში, ფაქტია რომ ამგვარი გარჩევით რომელიც აქ დევს upsolving-ში ამოცანა იჭრება.