გარჩევის pdf ვერსიის სანახავად მიჰყევით ამ ბმულს.
| # | ამოცანა | ავტორი |
| A | numbers | ელდარ ბოგდანოვი |
| B | timediff | ანდრეი ლუცენკო |
| C | knight | გიორგი საღინაძე |
| D | suggestions | დავით რაჭველიშვილი |
| E | mazesol | ელდარ ბოგდანოვი |
ერთადერთი გამონაკლისი შემთხვევაა N=1. აქ ჩვენ გვიწევს ანგარიში გავუწიოთ რიცხვს 0, ვინაიდან ის ერთციფრიანია და ამ ციფრის მოცილება აღარ შეიძლება. ამიტომ N=1-ისთვის ამოცანის პასუხი, როგორც მაგალითიდანაც ჩანდა, 10-ის ტოლია.
გარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.
იმის გამო რომ დროის ფორმატში გვაქვს ':' სიმბოლო პირდაპირ რიცხვად ვერ წავიკითხავთ მონაცემებს. უნდა წავიკითხოთ სტრიქონი მთლიანად და შემდეგ რამენაირად გამოვყოთ იქიდან რიცხვები. ამის გასაკეთებლად არის უამრავი გზა, მე განვიხილავ ყველაზე მარტივ ვარიანტებს:
1. შევცვალოთ ':' სიმბოლოები ჰარებით და შემდეგ გამოვიყენოთ sscanf, istringstream.
2. დავყოთ სტრიქონი ':' სიმბოლოს მიხედვით (Java-ში split) და მიღებული ნაწილები პირდაპირ გადავაქციოთ მთელ რიცხვებად (C/C++: atoi(); Java: Integer.valueOf() ).
3. ეს ხერხი ყველა ენაში გამოდგება, მაგრამ არაა მაინც და მაინც მარტივი და შეცდომის დაშვების ალბათობა იზრდება. რადგან ციფრების პოზიციები ზუსტადაა ცნობილი პირდაპირ შევადგინოთ რიცხვები:
int H=10*(S[0]-'0')+(S[1]-'0');
int M=10*(S[3]-'0')+(S[4]-'0');
int S=10*(S[6]-'0')+(S[7]-'0');სხვაობის გამოთვლა. იმისთვის რომ მარტივად გამოვთვალოთ სხვაობა გადავიყვანოთ დრო წამებში. ფორმულა ტრივიალურია T=H*60*60+M*60+S. დროის T1 და T2 მომენტებს შორის იქნება T2-T1 თუ T2>T1 და T2-T1+24*60*60 წინააღმდეგ შემთხვევაში (ანუ ეს ის შემთხვევაა, როდესაც სხვადასხვა კალენდარულ დღეებშია შეკითხვა დასმული და პასუხი გაცემული, ამიტომ ერთი დღეღამე უნდა დავუმატოთ).
სხვაობა d დათვლილია, ახლა უნდა გამოვიტანოთ პასუხი. სულ გვაქვს H=d/60/60 საათი, M=(d/60)%60 წუთი და S=d%60 წამი (პასკალის მოყვარულებისთვის განვმარტავ % ნიშანს, ეს არის მოდულის აღების ოპერაცია ანუ mod პასკალში). იმის მერე რაც გამოვთვალეთ კომპონენტები დანარჩენი ტრივიალურია. თუ კომპონენტი 0-ის ტოლი არაა გამოგვაქვს:
if(H)printf("%d saati ",H);
if(M)printf("%d tsuti ",M);
if(S)printf("%d tsami\n",S);გარჩევა მომზადებულია ანდრეი ლუცენკოს მიერ.
უპირველესყოვლისა, შევნიშნოთ, რომ ერთი ფერის უჯრაზე დასმული მხედარი თავისი ფერის უჯრებს არ ემუქრება.
მარტივი მისახვედრია, რომ ისეთი დაფებისათვის, რომელთა სვეტების და სტრიქონების რაოდენობა მეტია ორზე, მხედრების ოპტიმალური განლაგება მიიღწევა მათი ერთი ფერის უჯრებზე დასმით.
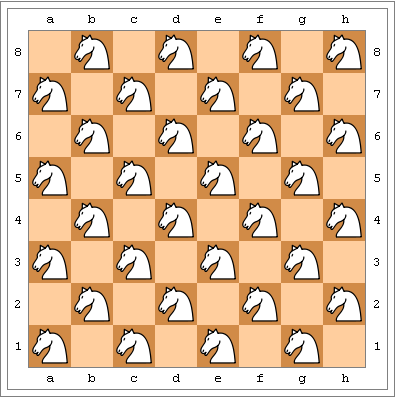
ანუ N სტრიქონისა და M სვეტისაგან შედგენილ დაფაზე (N,M > 2) დავსვამთ (N*M + 1) / 2 რაოდენობის მხედარს ამოცანის პირობის გათვალისწინებით.
ვაჩვენოთ რომ ეს პასუხი არის ნამდვილად მაქსიმალური:
დავაწყვილოთ დაფის უჯრედები ისე, რომ ყოველი წყვილი ერთმანეთს ემუქრებოდეს და თითოეული უჯრა შედიოდეს მხოლოდ ერთ წყვილში. ხოლო იმ შემთხვევაში როცა დაფის უჯრედების რაოდენობა კენტია დავაწყვილოთ ყველა უჯრა 1 ის გარდა. ასეთი დაწყვილების პოვნა ყოველთვის შეიძლება.
რადგანაც ყოველი წყვილიდან მხოლოდ ერთ უჯრაზე არის შესაძლებელი მხედრის დასმა, ცხადია რომ პასუხი ვერ იქნება N*M / 2 - ზე (წყვილების რაოდენობა) მეტი როცა უჯრების რაოდენობა ლუწია და N*M / 2 + 1 - ზე მეტი, როცა უჯრების რაოდენობა კენტია.
დავუშვათ რომ N არ აღემატება M- ს და განვიხილოთ დარჩენილი კერძო შემთხვევები:
1. N = 1, პასუხი არის M, ერთ სტრიქონში დასმული მხედარი იმავე სტრიქონში არ ემუქრება არც ერთ უჯრას.
2. N = 2. ამ შემთხვევაში გვრჩება დაუწყვილებელი უჯრები როცა M არ იყოფა 4 ზე. ამ დროს მაქსიმალური პასუხი შეიძლება იყოს წყვილების რაოდენობას დამატებული დაუწყვილებელი უჯრედების რაოდენობა. ზუსტად ასეთ პასუხს მივიღებთ, თუ მხედრებს დავალაგებთ 2x2 ბლოკებად, ისე როგორც სურათზეა ნაჩვენები.

გარჩევა მომზადებულია გიორგი საღინაძის მიერ.
პირველი მეთოდით ამ ამოცანის ამოხსნისათვის საჭიროა შემოსული სიტყვების სიმრავლე დავასორტიროთ ლექსიკოგრაფიულად ზრდადობით. შემდეგ უკვე საჭიროა გვქონდეს ორი ინდექსი L და R რომელიც წარმოადგენს მომხმარებლის მიერ აკრეფილი მიმდინარე ტექსტის შესაბამისი სიტყვების მიმდევრობის პირველ და ბოლო ინდექსს დასორტირებულ მასივში. ყოველი ახალი სიმბოლოს აკრეფის შემდეგ უნდა მოხდეს ინდექსების განახლება და სიმბოლოს წაშლის შემდეგ უნდა დავბრუნდეთ წინა ეტაპზე დაგენერირებულ ინდექსებზე. ვინაიდან ჩვენი მასივი დასორტირებულია, ინდექსების განახლებისთვის შეგვიძლია გამოვიყენოთ ორობითი ძებნა.
ამ ალგორითმის რეალიზებისას კარგად უნდა დაამუშავოთ შემთხვევა, როდესაც აკრეფილ ტექსტს ან სიმბოლოს წაშლისას მიღებულ ტექსტს არცერთი სიტყვა არ შეესაბამება.
მეორე მეთოდი პირველზე გაცილებით ადვილია დასაწერად და ასევე უფრო ოპტიმალურიც არის. პირველ რიგში განვიხილოთ თუ რა არის მონაცემთა სტრუქტურა Trie და ამის შემდეგ უკვე ადვილად წარმოვიდგენთ ამოხსნას. Trie არის ხე, რომლის წიბოებზე წერია ასოები, ხოლო წვეროში წერია ის სიტყვა, რომელიც მიიღება ხის სათავიდან ამ წვერომდე სიარულისას შემხვედრ წიბოებზე დაწერილი ასოების კონკატენაციით.
ადვილად წარმოდგენისათვის იხილეთ Trie ხის სურათი, რომელიც აგებულია {Java, Rad, Rand, Raum, Rose} სიტყვების სიმრავლით.
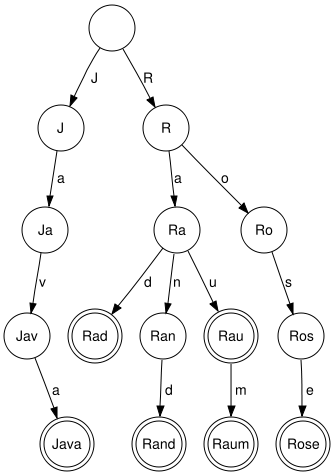
გარჩევა მომზადებულია დავით რაჭველიშვილის მიერ.
გამოვყოთ გასავლელი უჯრედების მიმდევრობიდან ერთი მიმართულებით სიარულის უწყვეტი შუალედები. მაგალითისთვის გავიხსენოთ პირობაში მოცემული ტესტი:
.X.S
...X
.X.X
.X.X
.X.X
.X.X
.X.X
.X.X
EX..ვინაიდან ყოველი ფერის კარტი ერთ მიმართულებას შეესაბამება და სხვაზე ვერ ახდენს ზეგავლენას, ჩვენ შეგვიძლია ოთხივე მიმართულება დამოუკიდებლად განვიხილოთ. მოცემულ მაგალითში, საკმარისია გამოვთვალოთ, რამდენნაირად შეიძლება ჯვრებით ისეთი პასიანსის გაშლა, რომელიც {1 მარცხნივ, 2 მარცხნივ} ნაწილს შეესაბამება და რამდენნაირად შეიძლება გულებით {1 ქვევით, 7 ქვევით} მიმდევრობის შესაბამისი პასიანსის გაშლა. საბოლოო პასუხი მათი ნამრავლი იქნება. საზოგადოდ, ამოცანის პასუხი ოთხივე მიმართულებით გასავლელი მიმდევრობების შესაბამისი პასიანსების რაოდენობათა ნამრავლია.
განვიხილოთ, როგორ შეიძლება პასუხის დათვლა ყოველი ცალკეული მიმართულებისთვის. პირველ რიგში, შევნიშნოთ, რომ თუ კონკრეტული მონაკვეთის გავლა შეიძლება რაღაც {A1, A2, ..., AK} კარტების სიმრავლით, მაშინ ისინი რა მიმდევრობითაც არ უნდა დავდოთ, შედეგად მაინც ამ მონაკვეთის ბოლო წერტილში აღმოვჩნდებით. ანუ ამ მონაკვეთის გავლა კარტების ამ სიმრავლის გამოყენებით K!-ნაირად არის შესაძლებელი. შედეგად ჩვენ უკვე შეგვიძლია ასეთი ალგორითმის შემოთავაზება: გადავარჩიოთ, კარტების რა სიმრავლე გამოვიყენოთ პირველი მონაკვეთის გასავლელად, რა სიმრავლე (დარჩენილი კარტების) გამოვიყენოთ მეორის გასავლელად და ასე შემდეგ ყველა მონაკვეთისთვის. ყოველი ასეთი სიმრავლეთა კრებულისთვის [ {A1,A2, ...,A|A|}, {B1,B2, ...,B|B|}, ..., {X1,X2,....,X|X|} ] კარგი პასიანსების რაოდენობა იქნება ტოლი (|A|! * |B|! * ... * |X|!)-ის, სადაც |S| S სიმრავლის სიმძლავრეს აღნიშნავს. ერთი მიმართულებისთვის პასიანსების რაოდენობა არის მისი მონაკვეთებისთვის ყველა ასეთი სიმრავლეთა კრებულისთვის პასუხების ჯამი.
მაგრამ ასეთ კრებულთა რაოდენობა შეიძლება საკმაოდ დიდი აღმოჩნდეს. ალგორითმის ოპტიმიზაციისთვის უნდა მივმართოთ ე.წ. დინამიურ პროგრამირებას. დინამიური პროგრამირება არ წარმოადგენს რამე კონკრეტულ ალგორითმს - ესაა ტექნიკა, რომელიც გულისხმობს ამოცანაში ისეთი ქვეამოცანების გამოყოფას, რომლების ანალიზი ბევრჯერ გვიწევს სრული ამოცანის ამოხსნის დროს და მსგავსი ქვეამოცანების ერთხელ ამოხსნის შედეგების დამახსოვრებას შემდგომი გამოყენებისთვის.
განვიხილოთ ასეთი სიტუაცია: კონკრეტული მიმართულებისთვის გვაქვს 2 მონაკვეთი სიგრძეებით 8 და 13. ზემოთხსენებული სიმრავლეების კრებულებთა შორის გვექნება შემდეგი ორი: [ {1,3,4}, {2,5,6} ] და [ {1,2,5}, {3,4,6} ]. როგორც ხედავთ, ჯამში ამ ორ მონაკვეთზე ასეთ შემთხვევაში ვხარჯავთ სიმრავლეს {1,2,3,4,5,6}. ამ ორის შემდეგ კიდევ რამოდენიმე მონაკვეთი რომ იყოს, ალგორითმის დარჩენილი ნაწილისთვის არანაირი მნიშვნელობა აღარ აქვს, კონკრეტულად რომელ მონაკვეთს რა კარტების სიმრავლე დასჭირდა - არსებითია მხოლოდ ის, თუ რა კარტებია უკვე გამოყენებული. ამიტომაც ამ ორი მონაკვეთის შემდეგ რა მონაკვეთებიც არ უნდა მოდიოდეს, [ {1,3,4}, {2,5,6} ] სიმრავლეებით დაწყებულ კრებულთა რაოდენობა ტოლია [ {1,2,5}, {3,4,6} ]-ით დაწყებულთა რაოდენობის და შესაბამისად მათთვის პასუხებიც ტოლია. მაშინ არაფერი გვიშლის, ამ პასუხის ერთხელ გამოთვლის შემდეგ დავიმახსოვროთ იგი და მეორედ რომ მივადგებით ანალოგიურ სიტუაციას, უბრალოდ გამოვიყენოთ ეს დამახსოვრებული მნიშვნელობა.
ფორმალურად, ჩვენ შეგვიძლია დავიმახსოვროთ პასუხები ყოველი წყვილისთვის {გავლილი მონაკვეთების რაოდენობა, გამოყენებული კარტების სიმრავლე}. მონაკვეთების რაოდენობა ვერ იქნება 52-ზე დიდი (ვინაიდან ყოველს 1 მაინც კარტი სჭირდება, წინააღმდეგ შემთხვევაში ამოცანის პასუხი 0-ია), ხოლო სიმრავლეების რაოდენობა 2^13-ია. ყოველი ასეთი წყვილისთვის დაგვჭირდება გამოუყენებელი კარტების ყველა სიმრავლის შემოწმება და მათგან ისეთების ამორჩევა, რომლებში შესული კარტების ჯამური ღირებულება შემდეგი მონაკვეთის სიგრძის ტოლია. ყველა შესაძლო სიმრავლისთვის მათი ქვესიმრავლეების რაოდენობების ჯამი 3^13-ის ტოლია, ამიტომ მთლიანობაში ერთი მიმართულებით პასუხის გამოთვლას 52*3^13-ზე ოპერაციაზე მეტი არ დასჭირდება.
ბოლოს ერთი-ორი სიტყვა ვთქვათ პასუხის შენახვის თაობაზე. ამოცანის პასუხი ნებისმიერ სტანდარტულ საბაზისო მთელ ტიპს აღემატება, ამიტომ მისი გამოთვლა და ბოლოში 1,000,000,009-ზე გაყოფა არაა მიზანშეწონილი. ცხოვრება შეგვიძლია გავიმარტივოთ მოდულარული არითმეტიკის თვისებების გამოყენებით. კერძოდ, ნებისმიერი მთელი A და B რიცხვების ჯამი და ნამრავლი ექვემდებარება შემდეგ ფორმულებს:
(A+B) mod M = ((A mod M) + (B mod M)) mod M
(A*B) mod M = ((A mod M) * (B mod M)) mod Mგარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.




