გადავწყვიტეთ, რომ ამოცანების გარჩევები pdf ვერსიის გარდა პოსტის სახითაც გამოვაქვეყნოთ.
| # | ამოცანა | ავტორი |
|---|---|---|
| A | words | დავით რაჭველიშვილი |
| B | cities | ანდრეი ლუცენკო |
| C | life | დავით რაჭველიშვილი |
| D | candy | გიორგი ლეკვეიშვილი |
| E | voyage | ელდარ ბოგდანოვი |
ამოცანა A. "საჩათაო სიტყვები"
ავაგოთ მოცემული ამოცანის მათემატიკური მოდელი. მას შემდეგი სახე ექნება: გვაქვს N ცალი ობიექტი და საპოვნელია, რამდენნაირად შეიძლება 2 განსხვავებული ობიექტის ამორჩევა ისე, რომ ობიექტების მიმდევრობას მნიშვნელობა ჰქონდეს.
ამ ამოცანის ამოსახსნელად გამოვიყენოთ კომბინატორიკის ერთ–ერთი საბაზისო ფორმულა A(n,k), სადაც n განსაზღვრავს ობიექტების რაოდენობას, ხოლო k მიუთითებს, რამდენი ობიექტი უნდა ამოვარჩიოთ:
A(n, k) = n! / (n-k)!ჩვენ შემთხვევაში K=2 და მივიღებთ:
A(n, 2) = n! / (n-2)! = n*(n-1)ამგვარად, ჩვენი ამოცანის პასუხი მოცემული N–ისთვის არის N*(N-1).
ალტერნატიული მიდგომა:
კომბინატორიკის ცოდნის გარეშე შესაძლებელია ამ ამოცანას მივუდგეთ სხვაირად. ავიღოთ სიტყვის პირველ ასოდ ანბანის ნებისმიერი ასო. მაშინ მეორე ასოს ამორჩევა შეიძლება (N-1)–ნაირად, ვინაიდან ასოები არ უნდა ემთხვეოდეს. საბოლოოდ გამოგვდის ისევ N*(N-1).
გარჩევა მომზადებულია დავით რაჭველიშვილის მიერ.
ამოცანა B. "ქალაქობანა"
ამ ამოცანის მთავარი სირთულე იყო შემომავალი მონაცემების სწორად წაკითხვა. საოლიმპიადო ამოცანებში ხშირად გვხვდება სიტუაცია, როდესაც არ არის მოცემული მონაცემების რაოდენობა და გვჭირდება წავიკითხოთ მონაცემები ფაილის ბოლომდე. ამისთვის სხვადასხვა ენაში არსებობს სხვადასხვა ხერხები. განვიხილოთ სტანდარტული C:
#include <string.h>
#include <stdio.h>
char toupper(char c){
if (c>='a' && c<='z') c+='A'-'a';
return c;
}
int main() {
freopen("cities.in","r",stdin);
freopen("cities.out","w",stdout);
char a[51],b[51];
int ans=0;
scanf("%s",a);
while(scanf("%s",b)!=EOF) {
if (toupper(a[strlen(a)-1])!=b[0]) ans++;
strcpy(a,b);
}
printf("%d\n",ans);
return 0;
while(scanf("%s",b)!=EOF)ასევე შემოვიღე ფუნქცია toupper, რომელიც აბრუნებს იგივე სიმბოლოს, რაც გადაეცა პარამეტრად, ოღონდ მაღალ რეგისტრში. ერთასოიანი ქალაქის შემთხვევაში (ამოცანის პირობის თანახმად ეს დაშვებულია) ფუნქციას გადაეცემა სიმბოლო უკვე მაღალ რეგისტრში და ის დაბრუნდება უცვლელად.
ანალოგიური ამოხსნა c++-ზე უფრო ლამაზი გამოდის:
#include <iostream>
#include <string>
using namespace std;
int main() {
freopen("cities.in","r",stdin);
freopen("cities.out","w",stdout);
string a,b;
int ans=0;
cin>>a;
while(cin>>b) {
if (toupper(a[a.length()-1])!=b[0]) ans++;
a=b;
}
cout<<ans<<endl;
return 0;
}გავრცელებულია შემდეგი სახის შეცდომა:
...
while(!feof(stdin)){
scanf("%s",s);
...
}
...
ამ შემთხვევაში თუ არ შეამოწმებთ scanf-ის შედეგს ორჯერ გაგიმეორდებათ ბოლო წაკითხული სიტყვა: feof ფუნქციამ შეიძლება დაინახოს ფაილის ბოლოში CR/LF სიმბოლოები ან ჰარები და ამის გამო დააბრუნოს false, ხოლო scanf-ი ვერ წაიკითხავს ახალ სიტყვას და s-ში დარჩება ძველი შიგთავსი.
>Java-ზე დაწერა ყველაზე ადვილია:
import java.io.*;
import java.util.Scanner;
public class Main {
public static void main(String[] args) throws IOException {
Scanner in = new Scanner(new FileReader("cities.in"));
PrintWriter out = new PrintWriter(new FileWriter("cities.out"));
String a = in.next();
String b;
int ans = 0;
while (in.hasNext()) {
b = in.next();
if (a.toUpperCase().charAt(a.length() - 1) != b.charAt(0)) {
ans++;
}
a = b;
}
out.println(ans);
out.close();
}
}
და ბოლოს Pascal:
var
s : ansistring;
c , last : char;
i , j , k : integer;
function ischar(c : char) : integer;
begin
ischar := 0;
if (c >= 'a')and(c <= 'z') then
ischar := 1;
if (c >= 'A')and(c <= 'Z') then
ischar := 1;
end;
function toupper(c : char) : char;
begin
if (c >= 'a')and(c <= 'z') then c := chr(ord(c) - ord('a') + ord('A'));
toupper := c;
end;
begin
assign(input , 'cities.in'); reset(input);
assign(output , 'cities.out'); rewrite(output);
last := '0';
while not eof do
begin
readln(s);
i := 1;
while (i <= length(s)) do
begin
if ischar(s[i]) = 1 then
begin
if (toupper(s[i]) <> toupper(last)) and (last <> '0') then
k := k + 1;
while ((i <= length(s)) and (ischar(s[i]) = 1)) do
i := i + 1;
last := s[i - 1];
end else
i := i + 1;
end;
end;
writeln(k);
close(input);
close(output);
end.გარჩევა მომზადებულია ანდრეი ლუცენკოს მიერ.
ამოცანა C. "ცხოვრების თამაში"
ამოცანის შეზღუდვებიდან გამომდინარე, საკმარისი იყო ყოველი დღის სიმულაცია მოგვეხდინა და ექსპერიმენტის ბოლოს დაგვეთვალა ვირუსების რაოდენობა.
სიმარტივისათვის დაკვირვების გარემო უნდა აღგვეწერა როგორც სამ განზომილებიანი მასივი X[K][N][M], სადაც პირველი განზმილება მიუთიდებდა ექსპერიმენტის დღეს, ხოლო დანარჩენი ორი დაკვირვების გარემოს. ყოველი pos დღის მონაცემების დასაგენერირებლად გამოვიყენებთ pos-1 დღის შედეგებს.
for (int i = 0; i < n; i++){
for (int j = 0; j < m; j++){
env[pos][i][j] = env[pos-1][i][j];
int counter = 0;
for (int w = 0; w < 8; w++){
int a = i+way[w][0];
int b = j+way[w][1];
if (a >= 0 && b >= 0 && a < n && b < m) counter += env[pos-1][a][b];
}
if(env[pos-1][i][j]==0 && counter==3) env[pos][i][j]=1;
if(env[pos-1][i][j]==1 && (counter < 2 || counter > 3)) env[pos][i][j]=0;
}
}
მინდა შევნიშნო, რომ მოცემულ კოდში ყოველი მეზობელი უჯრის შემოწმება არ ხდება სათითაოდ დაწერილი ბრძანებებით, არამედ გამოყენებულია მასივი:
int way[8][2]= {{0,1},{0,-1}, {1,0}, {-1,0}, {1,1}, {-1,-1}, {1,-1}, {-1,1}};რომელშიც way[i][0] და way[i][1] მასივის ელემენტებში ჩაწერილნი არიან ის რიცხვები, რომლებიც მიმდინარე უჯრედის ინდექსებს უნდა დაემატოს, რათა გადავიდეთ მის i-ურ მეზობელზე. ეს მეთოდი გვაძლევს საშუალებას, რომ კოდი იყოს უფრო კომპაქტური და ნაკლები შანსი იყოს შეცდომის დაშვების.
გარჩევა მომზადებულია დავით რაჭველიშვილის მიერ.
ამოცანა D. "ტკბილეული"
ამოცანის პირობიდან ნათლად ჩანს, რომ ყოველ ჯერზე უნდა ავიღოთ ისეთი ტკბილეული, რომელსაც ზემოდან სხვა ტკბილეული არ ადევს, წინააღმდეგ შემთხვევაში ირაკლი დაისვრება. შესაბამისად ყოველი ტკბილეულის აღების შემდეგ თითოეული ტკბილეულისთვის უნდა ვიცოდეთ, თუ რამდენი ტკბილეული არის მის ზემოთ, რათა სწორი გადაწყვეტილება მივიღოთ.სანამ ამოხსნის ჩამოყალიბებაზე გადავალთ, შემოვიღოთ შემდეგი აღნიშვნა: ტკბილეულის ხარისხი ტოლია ისეთი ტკბილეულების რაოდენობის, რომლებიც უშუალოდ მას ადევს ზემოდან. მაგალითად ამოცანის პირველ მაგალითში პირველი ტკბილეულის ხარისხი არის 0, ხორო მეორესი 1.ამოხსნის ფსევდო კოდი:
- წავიკითხოთ მონაცემები;
- თითოეული ტკბილეულისთვის დავითვალოთ მისი ხარისხი;
- მანამ სანამ მაგიდაზე არის ერთი ტკბილეული მაინც:
- ავიღოთ ის ტკბილეული, რომლის ხარისხიც არის ნულის ტოლი;
- ყველა იმ ტკბილეულს, რომელსაც არჩეული ტკბილეული ედო ზემოდან, ხარისხი შევუმციროთ ერთით.
ამოხსნის გასაუმჯობესებლად შეგვიძლია გამოვიყენოთ მონაცემთა სტრუქტურა გროვები (Heap), რომელიც საშუალებას გვაძლევს ეფექტურად მოვახდინოთ რიცხვების სიმრავლიდან მინიმალურის ამორჩევა. გროვაში თითოეულ ოპერაციას (ჩამატება/ამოღება) სჭირდება O(log N) დრო, სადაც N ელემენტების რაოდენობის ტოლია. მისი გამოყენების შემთხვევაში ჩვენი ალგორითმის მუშაობის დრო გახდება O(M * log N), რაც დამაკმაყოფილებელია, თუმცა მოცემული ამოცანის შემთხვევაში არსებობს უფრო ეფექტური ამოხსნის გზები, ამიტომ ამ მიდგომაზე არ გავჩერდები. მსურველებს გროვების შესახებ შეგიძლიათ წაიკითხოთ Wikipedia-ს მისამართზე: en.wikipedia.org/wiki/Heap_(data_structure).
ვეცადოთ თავიდან აღნიშნული ალგორითმის გაუმჯობესებას, ამისათვის ჯერ შემოვიღოთ შემდეგი აღნიშვნები:
- ტკბილეულები ავღნიშნოთ როგორც გრაფის წვეროები;
- ტკბილეულების წყვილები, რომელთაგანაც ერთი ზემოდან ადევს მეორეს, აღვნიშნოთ როგორც გრაფის მიმართული (ორიენტირებული) წიბო პირველი წვეროდან მეორესკენ.
მოცემული გვაქვს გრაფი N წვეროთი და M მიმართული წიბოთი. ჩვენი ამოცანაა ყოველ ჯერზე გრაფიდან წავშალოთ ისეთი წვერო, რომლისთვისაც არ არსებობს მასში შემავალი წიბო (ხარისხი 0-ის ტოლია).
განვიხილოთ პირობაში მოცემული მეორე მაგალითი:
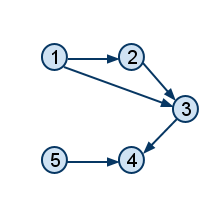 |
საწყისი გრაფი |
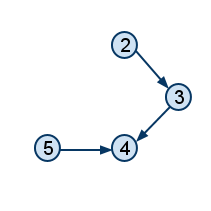 |
გრაფი პირველი წვეროს წაშლის შემდეგ |
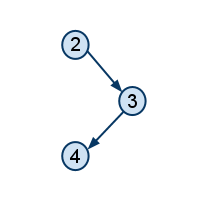 |
გრაფი მეხუთე წვეროს წაშლის შემდეგ |
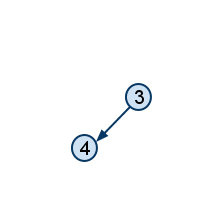 |
გრაფი მეორე წვეროს წაშლის შემდეგ |
 |
გრაფი მესამე წვეროს წაშლის შემდეგ |
| მეოთხე წვეროც წაიშალა |
პირველად აღნიშნულ ალგორთმში ყოველ ჯერზე გვიწევდა წვეროების გადარჩევა და მათ შორის ისეთის არჩევა, რომლის ხარისხიც არის 0-ის ტოლი, რაც საკმაოდ არაეფექტურია და საჭიროებს გაუმჯობესებას.
მისი გაუმჯობესების მიზნით შემოვიღოთ სია, რომელშიც შენახული გვექნება ყოველ ეტაპზე გრაფში იმ წვეროების ნომრები, რომელთა ხარისხიც არის 0-ის ტოლი. შესაბამისად ყოველ ჯერზე ამ სიიდან მოხდება ახალი წვეროს არჩევა.ჩვენი თავდაპირველი ალგორითმი მიიღებს შემდეგ სახეს:
- გრაფში თითოეული წვეროსთვის დავითვალოთ მისი ხარისხი;
- სიაში შევინახოთ 0 ხარისხის მქონე წვეროები;
- სანამ სია არაცარიელია:
- სიიდან ამოვიღოთ პირველი წვერო;
- ამოღებული წვერო წავშალოთ გრაფიდან და განვაახლოთ ყოველი მისი მეზობელი წვეროს ხარისხი;
- ყველა ის წვერო რომლის ხარისხიც გახდა 0-ის ტოლი ჩავამატოთ სიაში.
ამ ალგორითმის მუშაობის დრო არის O(N+M), რისთვისაც სავსებით საკმარისია 1 წამი.
განვიხილოთ ამოცანის ამოხსნის კიდევ ერთი გზა. თუ გრაფში წიბოების მიმართულებებს შევაბრუნებთ, მაშინ ამოცანის ამოხსნა შეიძლება რეკურსიულად სიღრმეში ძებნის DFS (Depth First Search) ალგორითმის გამოყენებით. დაწვრილებით შეგიძლიათ წაიკითხოთ Wikipedia-ს მისამართზე: http://en.wikipedia.org/wiki/Depth-first_search
სიტყვიერად მისი არსი მდგომარეობს შემდეგში:
- ყოველ ჯერზე ვირჩევთ ისეთ წვეროს, რომლის ხარისხიც არის 0-ის ტოლი;
- მიმდინარე წვეროსთვის ვამოწმებთ, ჰყავს თუ არა მას მეზობელი წვერო, რომელშიც ჯერ არ ვყოფილვართ;
- თუ კი, მაშინ გადავდივართ მეზობელ წვეროში
- თუ არა მაშინ ვბეჭდავთ მიმდინარე წვეროს ნომერს და ვბრუნდებით უკან იმ წვეროში საიდანაც აქ გადმოვედით და გადავდივართ მეორე ბიჯზე
საბოლოო ჯამში ამოცანა არის ტიპიური ტოპოლოგიური სორტირების (Topological Sorting) ამოცანა: http://en.wikipedia.org/wiki/Topological_sorting
ამოცანის ამოხსნასთან ასევე დაკავშირებულია მოცემული გრაფის ეფექტურად შენახვის პრობლემა. არსებობს მეხსიერებაში გრაფის შენახვის რამოდენიმე გზა:
- მეზობლების მატრიცა (Adjacency Matrix): ორგანზომილებიანი მასივი სადაც I-ური სტრიქონის J-ურ სვეტში წერია 1 თუ არსებობს წიბო I წვეროდან J წვეროსკენ და 0 წინააღმდეგ შემთხვევაში;
- მეზობლების სია (Adjacency List): ყოველი წვეროსთვის გვაქვს მისი მეზობლების სია, რომლის რეალიზებაც შეიძლება Linked List მონაცემთა სტრუქტურის გამოყენებით.
ჩვენს შემთხვევაში პირველი ვარიანტი არ გამოგვადგება, რადგან წვეროების მაქსიმალური რაოდენობა არის 50 000. შესაბამისად მატრიცის ზომა გამოვა 50 000 x 50 000, რაც 2384 მეგაბაიტის ტოლია, ჩვენ კი მხოლოდ 64 მეგაბაიტი მეხსიერების გამოყენება შეგვიძლია.
საკითხავი მასალა:
- Graph: en.wikipedia.org/wiki/Graph_(data_structure)
- DFS: en.wikipedia.org/wiki/Depth-first_search
- Topological Sorting: en.wikipedia.org/wiki/Topological_sorting
- Heap: en.wikipedia.org/wiki/Heap_(data_structure)
- Linked List: en.wikipedia.org/wiki/Linked_list
გარჩევა მომზადებულია გიორგი ლეკვეიშვილის მიერ.
ამ ამოცანის ამოსახსნელად პირველ რიგში იგი უნდა გადავიყვანოთ გრაფთა თეორიის ენაზე. გრაფის წვეროებად განვიხილოთ ქალაქები, ხოლო წიბოებად - ბილეთები. ვინაიდან ბილეთები არ ზღუდავენ, რომელი მიმართულებით შეიძლება მათი გამოყენება, გრაფი არაორიენტირებული გამოგვდის. თვითონ ამოცანის დავალება კი ამ აღნიშვნებში ასეთნაირად ჟღერს: ვიპოვოთ მინიმალური ზომის წიბოების სიმრავლე, რომელთა გრაფში ჩამატება უზრუნელყოფს შესაძლებლობას, რომ წვერო "ბათუმიდან" დავიწყოთ, გავიაროთ გრაფის ყველა წიბოზე და შედეგად ისევ დავბრუნდეთ წვერო "ბათუმში".
დახრილი შრიფტით გამოყოფილი პირობა წარმოადგენს გრაფთა თეორიის ერთ-ერთ ცნობილ თემას, კერძოდ კი ეილერის ციკლს. გრაფში ეილერის ციკლის არსებობა ნიშნავს, რომ მისი ნებისმიერი წვეროდანაა შესაძლებელი ყველა წიბოს შემოვლა და ამავე წვეროში დაბრუნება (ამ განსაზღვრებაში გამიზნულად არის გამოპარული უზუსტობა, რომელსაც შემდგომში დავუბრუნდებით). მართლაც, თუ განიხილავთ მოცემულ ამოცანაში რომელიმე მარშრუტს, რომელიც ბათუმში იწყება და მთავრდება და ყველა ბილეთს იყენებს, ადვილად დაინახავთ, რომ იგი ნებისმიერი სხვა ქალაქისთვისაც გამოსადეგია. მაგალითად, პირველ მაგალითის ტესტში ერთ-ერთი შესაძლო მარშრუტი იყო:
BATUMI -> ODESSA -> CONSTANTA -> ISTANBUL -> ODESSA -> TRABZON -> BATUMIრომ გვდომოდა ოდესიდან ანალოგიური თვისებების მარშრუტის შედგენა, შეგვეძლო წინა მარშრუტი "ჩამოგვეჩოჩა" მარცხნივ, ანუ მივიღებდით:
ODESSA -> CONSTANTA -> ISTANBUL -> ODESSA -> TRABZON -> BATUMI -> ODESSAგადავიდეთ არაორიენტირებულ გრაფში ეილერის ციკლის არსებობის პირობებზე. პირველ რიგში, გრაფში ეილერის ციკლის არსებობისთვის ყველა მისი წვერო, რომელსაც ერთი მაინც მეზობელი წიბო გააჩნია, ერთ ბმულ კომპონენტში უნდა იყოს. ეს ნათელია: თუ რომელიმე ორი ასეთი წვერო არაა ერთ ბმულ კომპონენტში, მაშინ ერთიდან მეორეში წიბოების გავლით ვერ მოვხვდებით და შესაბამისად ყველა წიბოს გამვლელ ციკლს ვერ შევკრავთ. მეორე პირობა კი ისაა, რომ ყოველი წვეროს ხარისხი ლუწი უნდა იყოს. ეს იქიდან გამომდინარეობს, რომ ჩვენი ციკლი ყოველ წვეროში რამდენჯერაც შედის, იმდენჯერვე უნდა გავიდეს. ირკვევა, რომ ეს ორი პირობა როგორც აუცილებელი, ასევე საკმარისიცაა გრაფში ეილერის ციკლის არსებობისთვის. მათი საკმარისობის დამტკიცება ამ გარჩევის ფარგლებს სცდება და თუ გაინტერესებთ, შეგიძლიათ მაგალითად აქ გაეცნოთ.
ახლა კი უშუალოდ ჩვენს ამოცანას მივუბრუნდეთ. ჯერ აგიხსნით, რა უზუსტობაზე იყო საუბარი ზედა ნაწილში. ფორმალურად, გრაფი შეიძლება არ იყოს ბმული და მაინც გააჩნდეს ეილერის ციკლი - ეს იმ შემთხვევაში, თუ მისი ყველა წიბო ერთ კომპონენტშია, ანუ ყველა დანარჩენი კომპონენტი იზოლირებულ წვეროს წარმოადგენს. მაგრამ ჩვენს შემთხვევაში ჩვენ გვჭირდება, რომ გრაფს გააჩნდეს ისეთი ეილერის ციკლი, რომელიც წვერო "ბათუმზე" გადის. ამას მნიშვნელობა აქვს იმ დროს, როდესაც ამოცანის გმირს არა აქვს მოგებული არც ერთი ბილეთი, რომელსაც "ბათუმი" აწერია, ანუ ამ ქალაქის შესაბამისი წვერო იზოლირებულია საწყის გრაფში.
მაშ ასე, პირველ რიგში შევეცადოთ, მივიღოთ საწყისი გრაფისგან ბმული გრაფი. ამისთვის ჯერ ვიპოვოთ მისი ბმული კომპონენტები და საჭიროების შემთხვევაში წვერო "ბათუმი"-ც ცალკე კომპონენტად განვიხილოთ. კომპონენტების შეერთებას ასე გთავაზობთ (რეალურად უამრავი ხარბი სტრატეგიით შეიძლება ამის ოპტიმალურად გაკეთება). ვთქვათ, K ცალი კომპონენტი გვაქვს ნომრებით A1, A2, ..., AK. შევაერთოთ ყოველი Ai (1 < i < c) კომპონენტი Ai-1 და Ai+1 კომპონენტებთან, ანუ შევკრათ ისინი ერთგვარ ჯაჭვში.
ორი კომპონენტის შესაერთებლად პირველი კომპონენტის რომელიმე წვერო უნდა დავაკავშიროთ წიბოთი მეორე კომპონენტის რომელიმე წვეროსთან. როდესაც კომპონენტში ერთი მაინც კენტი ხარისხის წვერო არის, ჩვენთვის ხელსაყრელია, ზუსტად ეს წვერო გამოვიყენოთ კომპონენტების შესაერთებლად, ვინაიდან ასე კენტხარისხიანი წვეროების რაოდენობა დაიკლებს. კერძოდ რომელ კენტი ხარისხის მქონე წვეროს ავირჩევთ, მნიშვნელობა არა აქვს. თუ კომპონენტში ყველა წვერო ლუწი ხარისხისაა, მაშინ მისი ნებისმიერი წვერო უნდა გამოვიყენოთ. ამით კენტხარისხიანი წვეროების რაოდენობას ვზრდით, მაგრამ სხვანაირად კომპონენტი ცალკე დარჩება.
მივიღეთ რა ბმული გრაფი, მასში კენტხარისხიანი წვეროების "გამოსწორება" უკვე მარტივი ამოცანაა. ჩვენ შეგვიძლია, ასეთი ნებისმიერი ორი წვერო ავიღოთ და შევაერთოთ წიბოთი. შედეგად ორივეს ხარისხი ლუწი გაუხდება და მათი განხილვა აღარ მოგვიწევს. ანალოგიურად გავაგრძელოთ მანამ, სანამ ყველა წვერო არ გახდება ლუწი ხარისხის. ეს ყოველთვის მოხდება, ვინაიდან გრაფში კენტხარისხიანი წვეროების რაოდენობა აუცილებლად ლუწია.
იმპლემენტაციის მხვრივ, ამოცანა არ მოითხოვდა რაიმე სასწაულებს და პრაქტიკულად ყველა ნაბიჯის შესრულება: გრაფის აგება და შენახვა, ბმული კომპონენების პოვნა, მათი შეერთება - არაოპტიმალური მეთოდებით შეიძლებოდა.
გარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.




