ესეც pdf ფორმატში გარჩევების ბმული, პარალელურად კი upsolving-ში შეგიძლიათ მოსინჯოთ ძალები :)

# ამოცანა ავტორი
A english ელდარ ბოგდანოვი
B bulbs გიორგი ლეკვეიშვილი
C product გიორგი საღინაძე
D outlets ელდარ ბოგდანოვი
E laser ელდარ ბოგდანოვი




ვინაიდან ალგორითმულად ამ ამოცანაში გასარჩევი არაფერია, განვიხილავ ერთი-ორ შეცდომას, რომელიც დაუშვეს C++-მონაწილეებმა.

ერთი საკმაოდ უსიამოვნო შეცდომა დაკავშირებული იყო სტრიქონის სიგრძესთან. C-ში სტრიქონი არის უბრალოდ char-ების მასივი და როგორც ყველა მასივს, მასაც აქვს სიგრძე. ამ მასივის ყოველი ელემენტი 1 სიმბოლოს შეესაბამება. მაგრამ ჩვენ თუ გვაქვს სტრიქონი char s[10], ეს ხომ არ ნიშნავს, რომ მხოლოდ 10-სიმბოლოიან სტრიქონებს შევინახავთ მასში? ამიტომ სტრიქონის დასასრულად ითვლება ის სიმბოლო, რომლის კოდი არის 0-ის ტოლი. შესაბამისად, s[10] რეალურად მხოლოდ 9 სიმბოლოს შეინახავს, ხოლო მე10 0-ის ტოლი უნდა იყოს, რომ კომპიუტერი მიხვდეს, სტრიქონი სად ბოლოვდება. ასე რომ ამ ამოცანაში 11 სიგრძის სტრიქონი იყო აღსაწერი, წინააღმდეგ შემთხვევაში რაიმე სახის შეცდომა ამოხტებოდა.

მეორე შეცდომა, რომელიც შევნიშნე, ანალოგიური იყო პირველი ეპიზოდის B ამოცანაში დაშვებული შეცდომების. ოლიმპიადებზე მიღებულია, რომ ფაილის ბოლო სტრიქონის შემდეგ ყოველთვის არის ახალ ხაზზე გადასვლის სიმბოლო და ის სისტემა, რომლითაც ამჟამად თქვენი ამოხსნები მოწმდება, მაგ ახალ ხაზზ ავტომატურად ამატებს. ამიტომ ის, ვინც სიმბოლ-სიმბოლო წაიკითხავდა შემომავალ მონაცემებს, ახალი ხაზის სიმბოლოსაც წაიკითხავდა და არასწორი დამუშავების შემთხვევაში პრობლემები გაუჩნდებოდა. თუმცა კონკრეტულად იმ ამოხსნას, რომელზეც მაქვს საუბარი, უარესი რამ მოუვიდა. თუ თქვენ გააკეთებთ ფაილების კონსოლზე გადამისამართებას და gets-ით მოახდენთ სტრიქონის წაკითხვას, იგი ახალი ხაზის სიმბოლოს მაგივრად ბოლოში 0-ს დაისვამს და ყველაფერი რიგზე იქნება. მაგრამ პირდაპირ ფაილებთან მუშაობის დროს უნდა გამოიყენოთ ფუნქცია fgets, რომელსაც პარამეტრად გადაეცემა ისიც, თუ რამდენი სიმბოლო უნდა წაიკითხოს. ეს ფუნქცია ახალ ხაზზე გადასვლის სიმბოლოსაც კითხულობს და შედეგად მაგალითად სტრიქონი "aaabc" გახდება "aaabc#10" და არასწორად დამუშავდება.


გარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.


N <= 1000 შეზღუდისთვის შეგვიძლია სიმულაცია გავუკეთოთ ადამიანების ქმედებებს:

for (int i = 1; i <= n; i++) { // თავიდან ყველა ნათურა ჩამქვრალია
    state[i] = 0;
}
for (int i = 1; i <= n; i++) { // i-ური ადამიანი
    for (int j = i; j <= n; j += i) { // ნათურები რომლის ღილაკებსაც აჭერს თითს
        state[j] = 1 - state[j];
    }
}
int sol = 0;
for (int i = 1; i <= n; i++) {
    if (state[i] == 1) sol++;
}

ამ ალგორითმის მუშაობის დრო არის (N + N/2 + N/3 + ... + N/(N-1) + 1), რისი მუშაობისთვისაც მოცემული შეზღუდვებით 1 წამი საკმარისია. მეტიც, ასეთი მიდგომა N<=10^6-ზეც კი იმუშავებდა.

მოდით ამოცანას შევხედოთ სხვა კუთხით: ღილაკზე ყოველი მეორე თითის მიჭერა, მის შესაბამის ნათურას აბრუნებს საწყის მდგომარეობაში, ანუ ის ქვრება. შესაბამისად ოთახიდან ბოლო ადამიანის გამოსვლის შემდეგ მხოლოდ ის ნათურები დარჩება ანთებული, რომელსაც კენტჯერ მიეჭირა თითი.

ყოველ ღილაკს მხოლოდ ის ადამიანები მიაჭერენ თითს რომელთა ნომერიც ღილაკის შესაბამისი ნათურის ნომრის ზუსტი გამყოფია. მაგალითად მე-6 ნათურის ღილაკს თითს მიაჭერენ პირველი, მეორე, მესამე და მეექვსე ადამიანები. შესაბამისად ჩვენი ამოცანაა ვიპოვოთ 1-დან N-მდე რიცხვებს შორის რამდენს ყავს კენტი რაოდენობის გამყოფი.

int sol = 0;
for (int i = 1; i <= n; i++) {
    int cnt = 0;
    for (int j = 1; j <= i; j++) {
        if (i % j == 0) cnt++;
    }
    if (cnt % 2 == 1) sol++;

}

ალგორითმის მუშაობის დრო არის O(N^2), რაც ასევე ეტევა 1 წამში, თუმცა წინა ალგორითმზე ნელია.

მაგრამ ცოტა დაფიქრების შემდეგ ადვილად შეგვიძლია მივხვდეთ, რომ კენტი რაოდენობის ზუსტი გამყოფი ყავთ მხოლოდ ზუსტ კვადრატებს. დამკტიცება:

განვიხილოთ რიცხვი x და ნებისმიერი მისი გამყოფი a, რადგან a არის x-ის გამყოფი ამიტომ x/a -ც ასევე x-ის გამყოფია. შესაბამისად თუ ნებისმიერი a-სთვის a != x/a, მაშინ x არ არის ზუსტი კვადრატი და მას ყავს ლუწი რაოდენობის გამყოფი. ხოლო თუ არსებობს ისეთი a, რომ a == x/a, ზე მაშინ x a-ს ზუსტი კვადრატია და მას ყავს კენტი რაოდენობის გამყოფი. განვიხილოთ მაგალითი x = 12:

a x/a
1 12
2 6
3 4
4 3
6 2
12 1

12 არ არის ზუსტი კვადრატი და მას ყავს 6 გამყოფი, ხოლო თუ განვიხილავთ x = 16:

ax/a
116
28
44
8 2
161

16 ზუსტი კვადრატია და მას აქვს 5 გამყოფი. შესაბამისად ჩვენი ამოცანის ამოხსნაა 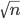\sqrt{n} : 

int sol = (int) floor(sqrt(n));

C/C++ -ში:
sqrt(x) = \sqrt{x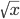} floor(x) = უდიდეს მთელ რიცხს რომელიც არ აღემატება x-ს, მაგალითად floor(0.5) = 0 ხოლო floor(-1.5) = -2.

გარჩევა მომზადებულია გიორგი ლეკვეიშვილის მიერ.



ამოცანა C. “ნამრავლი”


ცხადია, რომ ყველა რიცხვი, რომელიც მეტია 1-ზე, უნდა გამოვიყენოთ. მათი გამოყენებით ნამრავლიც იზრდება. ასევე უნდა გამოვიყენოთ ლუწი რაოდენობის უარყოფითი რიცხვები. აქ გასათვალისწინებელია, რომ -1-ს ვიყენებთ მაქსიმუმ ერთხელ, თუ -1 ზე ნაკლები ისიც იმ შემთხვევაში, თუ -1-ზე ნაკლები რიცხვების რაოდენობა კენტია. თუ დაფაზე დაწერილ რიცხვებს შორის არ არის -1 და უარყოფითი რიცხვების რაოდენობა კენტია, მაშინ მოდულით უმცირესი უარყოფითი რიცხვის გარდა ყველა უარყოფითს ვიღებთ.

გასათვალისწინებელია კერძო შემთხვევები:ამოცანა ითხოვს რომ მინიმუმ 1 რიცხვი მაინც იყოს არჩეული დაფიდან, ამიტომ შეიძლება პასუხი უარყოფითიც გამოვიდეს. მაგალითად თუ დაფაზე წერია -45 მაშინ პასუხიც იქნება -45.ზოგ შემთხვევაში შეიძლება 1 ის ან 0 ის აღებაც მოგვიწიოს. (-100 , 0) რიცხვების შემთხვევაში ვიღებთ 0 ს, (-1 , 0 , 0 , 1) - აქ კი მხოლოდ 1 ს.შესაძლებელია -1 იც ავიღოთ 2 ჯერ, (0 , 0 , -1 , -1) ტესტისთვის (-1,-1) გვაძლევს მაქსიმალურ ნამრავლს.

გარჩევა მომზადებულია გიორგი საღინაძის მიერ.



:



ბევრი მითქმა-მოთქმა გამოიწვია ქართულად "შტეფსელის" სწორ სახელს, მაგრამ ვინაიდან ჩემთვის "დენცქვიტა" თუ რაცაა კიდევ უფრო უცნაურად ჟღერს, ისევ შტეფსელს ვიტყვი ხოლმე :)

მაშ ასე, ამოცანის მცირე შეზღუდვები მიგვანიშნებს, რომ ამოხსნად შეიძლება გადარჩევამ ივარგოს. მოდით თავიდანვე ჩავთვალოთ, რომ N<=K, წინააღმდეგ შემთხვევაში შეგვიძლია ფიქტიური შტეფსელები დავამატოთ სადმე ოთახისგან ძალიან შორს და ვისაც ეგ შტეფსელი შეხვდება, რეალურად უშტეფსელოდ დარჩება. საერთოდ, "შუბლში ამოხსნა" იქნებოდა გადაგვერჩია ორგანიზატორებისთვის კაბელების გადანაწილების N! ვარიანტი და შტეფსელების გადანაწილების A(N,K) ვარიანტი და ყოველისთვის შეგვემოწმებინა, კაბელი რამდენს ეყო თავის შტეფსელამდე, მაგრამ ეს N=K=9 შემთხვევაში 9!*9!-ის რაოდენობა ვარიანტს მოგვცემს, რისი გადარჩევაც თანამედროვე კომპიუტერისთვის მცირე დროში არარეალურია. ვცადოთ ამ ორიდან მხოლოდ ერთი გადარჩევის ჩატარება და შემდეგ გავაკვირდეთ, რით შეიძლება მეორის ჩანაცვლება.

1) ვთქვათ, თავიდან გადავარჩიეთ, რომელი ორგანიზატორი რომელ კაბელს აიღებს. მაშინ ყოველი მათგანისთვის უკვე განსაზღვრულია, რომელ შტეფსელებს მიწვდება. გამოდის, რომ ყოველ ორგანიზატორს აქვს მისთვის ხელსაყრელი შტეფსელების სია და ორგანიზატორთა მაქსიმალურად რაოდენობას უნდა შევურჩიოთ შტეფსელი მისი სიიდან, რომელიც სხვას არავის მივეცით. ეს კი მაქსიმალური შეწყვილების პოვნის ამოცანაა.მაგრამ რადგან მისი ამოხსნა საკმაოდ შრომატევადია, მისი 9!-ჯერ გაშვება 1 წამში არ ჩაეტევა.

2) თავიდან გადავარჩიოთ, რომელ ორგანიზატორს რომელ შტეფსელს ვაძლევთ. მაშინ ჩვენ ფიქსირებული გვაქვს {A1, A2, ..., AN} სიგრძეების სია, სადაც Ai არის i-ური ორგანიზატორისგან მის შტეფსელამდე მანძილი.  შტეფსელების ამ გადანაწილებისთვის ოპტიმალური პასუხის მიღების ერთ-ერთი ვარიანტია მოვიქცეთ შემდეგნაირად: მივცეთ ყველაზე გრძელი კაბელი იმ ორგანიზატორს, რომლისგანაც თავის შტეფსელამდე მანძილი არ აღემატება ამ კაბელის სიგრძეს, მაგრამ მეტია (ან ტოლი) ყველა დანარჩენი ასეთი ორგანიზატორისთვის თავის შტეფსელამდე მანძილზე. სიგრძით მეორე კაბელსაც ასე მოვექცეთ, ოღონდ ის პირველი ორგანიზატორი მხედველობაში აღარ მივიღოთ, და ასე შემდეგ. ამ ალგორითმის იმპლემენტაცია შესაძლებელია ორივე სიის რიცხვების ზრდადობით დალაგებით და შემდეგ წრფივი გადავლით. მთელი ამოხსნის სირთულე გამოდის O(N! * NlogN) და ეს უკვე ეტევა 1 წამში.

კონტესტზე გატარებული პირველი ამოხსნა განსხვავებულ იდეაზე იყო აგებული. თუ ჩვენთვის ცნობილია პასუხი სამეულისთვის {ორგანიზატორების რომელიღაც ქვესიმრავლე, შტეფსელების რომელიღაც ქვესიმრავლე, გამოყენებული კაბელების რაოდენობა (კაბელები ფიქსირებული მიმდევრობითაა დალაგებული და i რაოდენობა ნიშნავს მიმდევრობის პირველ i ცალ კაბელს)}, დარჩენილ ორგანიზატორებსა, შტეფსელებსა და კაბელებში პასუხის საპოვნელად არ გვაინტერესებს, არსებულ არასრულ გადანაწილებაში ვის რომელი შტეფსელი და კაბელი ერგო. შესაბამისად, ამოცანის ამოხსნა შეიძლება დინამიური პროგრამირების საშუალებით, სადაც მდგომარეობა აღიწერება ზემოთ ნახსენები სამეულით.


გარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.



ლოგიკურია, რომ მშენებლობისთვის უნდა ავირჩიოთ ლაზერისგან მაქსიმალურად დაშორებული K უჯრედი. რუკის ზომა საშუალებას გვაძლევს, შევამოწმოთ ყველა უჯრედი და გამოვთვალოთ ყოველისთვის ენერგიის დანახარჯი, ხოლო შემდეგ დავალაგოთ მიღებული რიცხვები და უდიდესი K ცალი დავიტოვოთ.

შემდეგი ნაბიჯია იმის განსაზღვრა, რომელ უჯრედში ავაშენოთ ბაზები და რომლებში ელექტროსადგურები. ვინაიდან ლაზერი "ჭკვიანია" და ყოველთვის მინიმალურ ენერგიას დაახარჯავს მოთამაშის დამარცხებას, იგი გაანადგურებს ან ყველა ბაზას, ან ყველა ელექტროსადგურს – იმის მიხედვით, რის განადგურებას ჯამში ნაკლები ენერგია დასჭირდება. ანუ ჩვენი ამოცანაა ისე შევარჩიოთ ნაგებობათა ტიპები, რომ ამ ჯამურ ენერგიებს შორის უმცირესი რაც შეიძლება დიდი იყოს. რეალურად, ჩვენს წინაშე დადგა შემდეგი ამოცანა: რიცხვების მოცემული სია დავყოთ ორ ნაწილად ისე, რომ მათში შემავალი რიცხვების ჯამთა შორის მინიმალური იყოს რაც შეიძლება დიდი. ეს ტოლფასია იმისი, რომ ეს ჯამები ერთმანეთთან რაც შეიძლება ახლოს იყოს, რაც საკმაოდ გავრცელებულ ამოცანას წარმოადგენს.

ვინაიდან რიცხვების ზომები შემოსაზღვრულია და არ აღემატება 19602–ს (ამდენი ენერგია ლაზერს დასჭირდება, თუ იგი რუკის ერთ კუთხეშია, ხოლო გასანადგურებელი ნაგებობა დიამეტრალურად საწინააღმდეგო კუთხეში მდებარეობს), მათი ჯამი იქნება 19602*Kmax = 1,960,200–ზე ნაკლები. ამ შემთხვევაში ჩვენი ამოცანის ამოხსნა შეიძლება დინამიური პროგრამირების დახმარებით.

აღვნიშნოთ მიღებული K-რიცხვიანი სია S-ით (სიის ელემენტთა ინდექსირება 0-დან დაიწყოს). ასევე შემოვიღოთ ლოგიკური ფუნქცია F(i, j) ყველა მთელი i-სთვის [0, K] შუალედიდან და არაუარყოფითი მთელი j-ებისთვის, რომლის მნიშვნელობა იქნება ჭეშმარიტი, თუ სიის პირველი i ცალი რიცხვის რაიმე ქვესიმრავლით ჩვენ შეგვიძლია j ჯამის მიღება და იქნება მცდარი წინააღმდეგ შემთხვევაში. ცხადია, რომ 0 რიცხვით მხოლოდ 0-ის ტოლ ჯამს მივიღებთ, ამიტომ F(0,0)=true და F(0,j >0)=false. განვიხილოთ, როგორ შეიძლება F(i+1, j) მნიშვნელობების გამოთვლა, თუ ვიცით ყველა F(i, j). კონკრეტული j-სთვის F(i+1, j) არის ჭეშმარიტი მაშინ და მხოლოდ მაშინ, თუ სრულდება ერთ-ერთი:
1) F(i, j) არის ჭეშმარიტი. განსაზღვრების თანახმად, ეს ნიშნავს, რომ პირველი i რიცხვის რაღაც ქვესიმრავლის ელემენტთა ჯამი j-ს ტოლია. მაშინ პირველი (i+1) რიცხვის იგივე ქვესიმრავლითაც მაგ ჯამს მივიღებთ.
2) F(i, j-S[i]) არის ჭეშმარიტი (რა თქმა უნდა, უნდა სრულდებოდეს j>=S[i]). თუ პირველი i რიცხვის რაღაც ქვესიმრავლით შესაძლებელია (j-S[i]) ჯამის მიღება, მაშინ i-ური რიცხვის დამატებით ამ ქვესიმრავლეში მისი ჯამი ზუსტად j გახდება.

ცხადია, რომ ყველა რიცხვის ჯამზე უფრო დიდი j-ებისთვის F(i, j) ყოველთვის false არის, ამიტომ ამის იქით მისი შეფასება ტრივიალურია. შედეგად შეგვიძლია F-ის მნიშვნელობები ორგანზომილებიან მასივში შევინახოთ და ისინი იტერაციულად, მცირე i-ებიდან დიდებისკენ ვითვალოთ. ფუნქციის ჭეშმარიტი მნიშვნელობების პოვნისას ასევე შეგვიძლია შესაბამისი ქვესიმრავლის ელემენტებიც დავიმახსოვროთ. ჩვენ კიდევ ერთი სირთულე შეგვხვდება - ცხრილი სრულად 64MB-ში არ ჩაეტევა. მაგრამ ვინაიდან ყოველი i-სთვის F(i+1, j) მნიშვნელობები მხოლოდ F(i, j)-ს საფუძველზე ითვლება, შეგვიძლია უფრო ადრინდელი მნიშვნელობები აღარ დავიმახსოვროთ.

მოვახერხეთ რა F ფუნქციის მნიშვნელობების გამოთვლა, თავდაპირველი ამოცანაც გადაწყვეტილია. პასუხი ისეთი უდიდესი j იქნება, რომელიც არ აღემატება K რიცხვის ჯამის ნახევარს და რომლისთვისაც სრულდება F(K, j)=true - ანუ, სხვა სიტყვებით რომ ითქვას, ყველა რიცხვის რაიმე ქვესიმრავლის მაქსიმალური შესაძლო ჯამი, რომელიც არ აღემატება რიცხვების ჯამის ნახევარს. ასეთ ქვესიმრავლეში შესული რიცხვები რა უჯრედებსაც შეესაბამებოდა, იმათში ბაზებს ავაშენებთ, ხოლო რიცხვების სრული სიმრავლის დანარჩენი ელემენტების შესაბამის უჯრედებში კი ელექტროსადგურებს.

აღწერილ დინამიური პროგრამირების მეთოდს ხშირად "ზურგჩანთას" ეძახიან ხოლმე. დაწვრილებით ამის შესახებ შეგიძლიათ ვიკიპედიაზე და ტოპკოდერზე წაიკითხოთ.


გარჩევა მომზადებულია ელდარ ბოგდანოვის მიერ.